Van Emde Boas Trees

1. Problem

1. Maintain an ordered set of elements to support

• Membership (search)
• Successor/predecessor
• Insert/delete

2. Most well-known solutions: balanced search trees

$\Theta(\log n)$ time for $O(n)$ space

3. Lower bound for membership (search) under the binary decision tree:

$\Omega(\log n)$

Binary decision tree model

• Any algorithm is modelled as a binary tree where each node is labelled $x < y$
• Program execution corresponds to a root-leaf-path
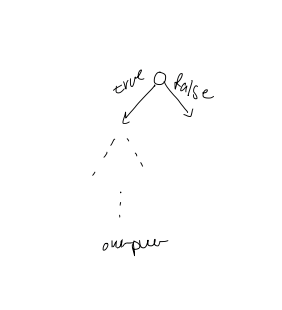
• Decision trees correspond to algorithms that only use comparisons to gain knowledge about input

Proof: Any binary decision tree for membership must have at least $n + 1$ leaves, one for each element + "not found". As a binary tree on $n+1$ leaves must have $\Omega(\log n)$, this lower bound applies.

4. "Counterexample": dynamic perfect hashing

Perfect hashing: every element can be searched for in $O(1)$ time but it doesn't support insert/delete.

Dynamic perfect hashing: can support insert/delete.

Membership: $O(1)$ worst-case Insert/delete: $O(1)$ amortized expected time Space: $O(n)$

5. Contradiction? Not really ... different machine models

RAM use input value as memory addresses, unlike binary decision tree model.

2. Model

1. Word RAM

• This model tries to model a realistic computer
• Word size $w \geq \log n$
• $O(1)$ "c-style" operations

2. Universe size: $u$

• Elements have values in the set ${ 0, 1, \dots, u-1 }$
• Elements fit in a machine word: $w \geq \log u$

3. Preliminary Approaches

1. Direct Addressing

Bit vector: $u = 16$, $n=4$, $S = { 1, 9, 10, 15 }$ 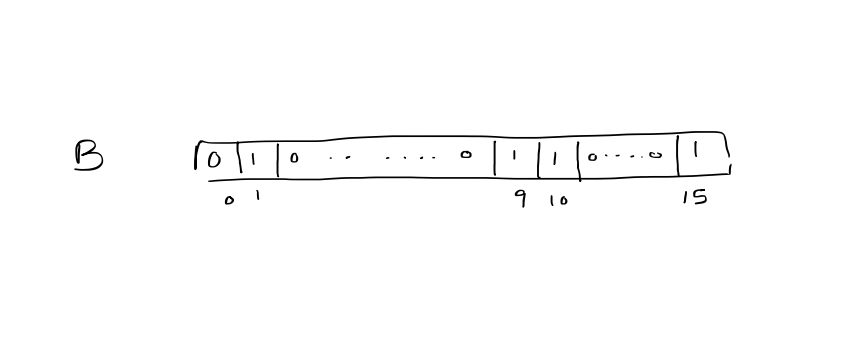$Insert / Delete / Membership: O(1)$ $Successor / predecessor: O(u)$

2. Carve into widgets of size $\sqrt{ u }$

$\rightarrow$ Assume that $u = 2^{2k}$

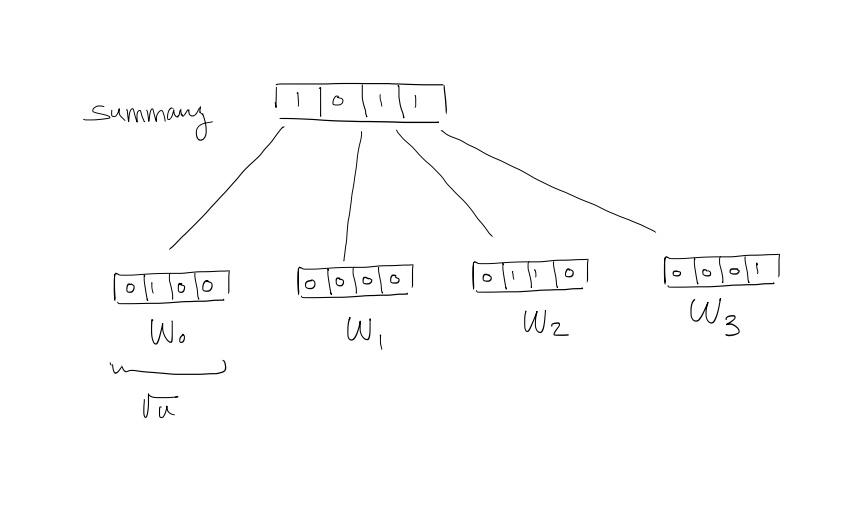$W_{i}[j]$ denotes $i\sqrt{ u } + j$, $j=0, 1, \dots , \sqrt{ u } -1$ $Summary[j] = 1 \iff$ $W_{i}$ contains at least a $1$

• $high(x) = \left\lfloor \frac{x}{\sqrt{ u }} \right\rfloor$
• $low(x) = x \mod{\sqrt{ u }}$

Both are $O(1)$.

• $x = high(x) \cdot \sqrt{ u } + low(x)$
• When $x$ is represented as a $\log u$-bit binary number, $high(x) =$ most significant $\frac{\log u}{2}$ bits $low(x) =$ lowest ...

Example $x = 9 \rightarrow 1001$ $high(x) = 10$ $low(x) = 01$ $Membership(x) = W_{high(x)}[low(x)] = W_{2}[1]$ Check if true!

$\text{successor}(x)$ Search to the right within $x$'s widget If we find a $1$, that position gives us the result Otherwise, search to the right within the summary If we find a $1$, that gives us the widget containing the Successor Scan that widget for the leftmost $1$

$\text{Insert/Delete}:$ widget, summary $\text{Insert:}O(1)$ because we simply set that but to $1$ and set its summary bit to $1$ if unset $\text{Delete}: O(\sqrt{ u })$: because we might have to scan the widget to see if there are any other $1$s, and unset the summary bit as needed

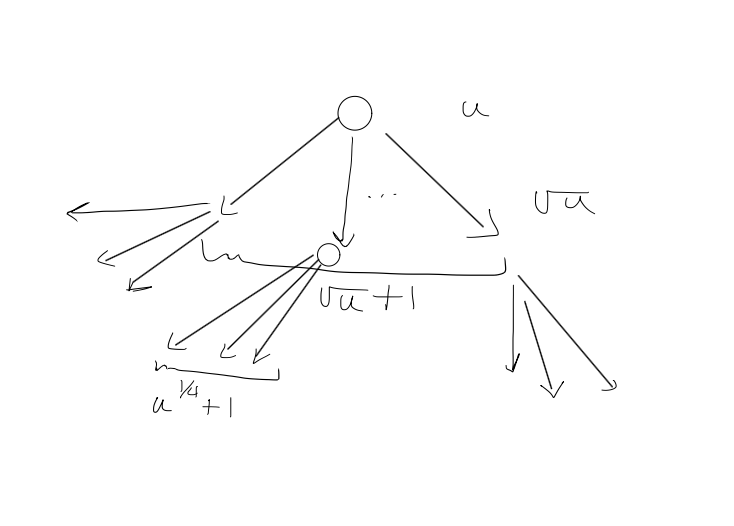
4. A recursive structure

1. $T(u) = T(\sqrt{ u }) + O(1)$

Let $m= \log u$, so that $u=2^m$

So that the recurrence becomes $$T(2^m) = T(2^{\frac{m}{2}}) + O(1)$$ Rename $S(m) = T(2^m)$ so that it becomes $$S(m) = S\left( \frac{m}{2} \right) + O(1)$$ Using the Master theorem, we can solve this as $$S(m) = O(\log m)$$ Change from $S(m)$ to $T(u)$ $$T(u) = T(2^m) = S(m) = O(\log m) = O(\log \log u)$$

2. Widget $W$

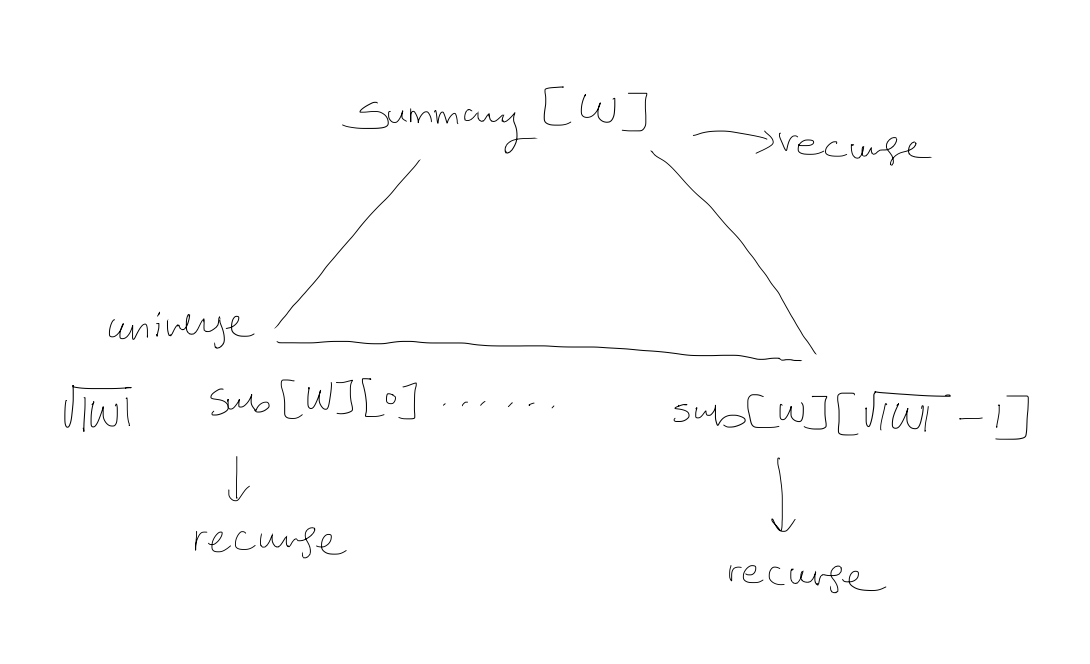
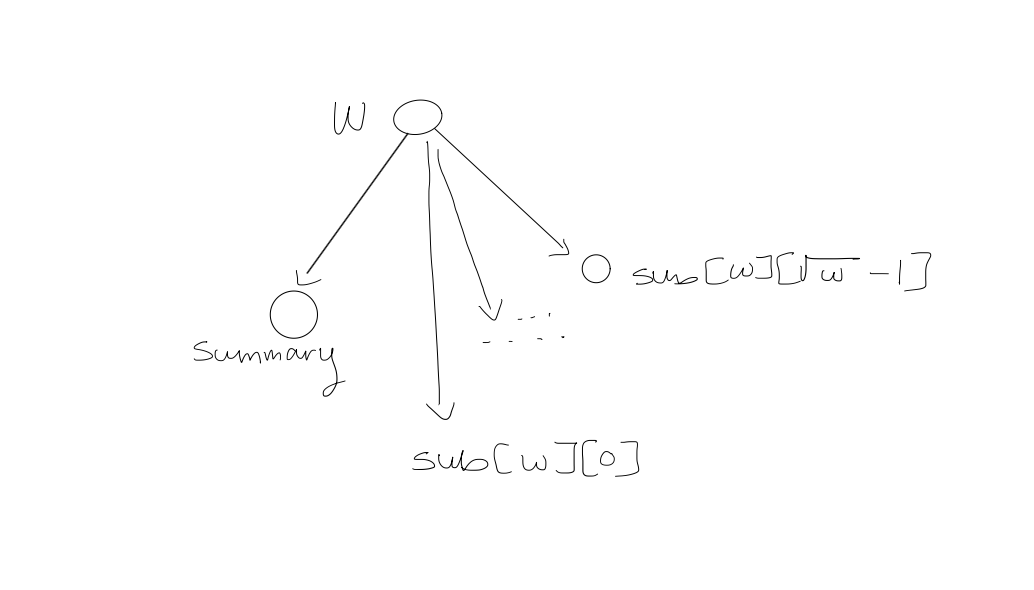
Base case: $W$ has $2$ bits

3. $\text{Member}(W,x)$

if $|W| = 2$ return $W[x]$ else return $\text{Member}(\text{sub}[W][\text{high}(x)], \text{low}(x))$

Since we are only making $1$ recursive call, the recurrence for this is $$T(u) = T(\sqrt{ u }) + O(1)$$ And so, the running time is $O(\log \log u)$

4. $\text{Insert}(W, x)$

if $|W| = 2$ $W[x] =1$ else $\text{Insert}(\text{sub}[W][\text{high}(x)], \text{low}(x))$ $\text{Insert}(\text{summary}[W], \text{high}(x))$

Since we make $2$ recursive calls, the recurrence for this is $$T(u) = 2T(\sqrt{ u }) + \Theta(1)$$ Let $m= \log u$, so that $u=2^m$ so that the recurrence becomes $$\begin{aligned} T(2^m) &= 2T(2^{m/2}) + \Theta(1) \ S(m) &= T(2^m) \ S(m) &= 2S\left( m/2 \right) + \Theta(1) \ S(m) &= \Theta(m) \ T(u) &= T(2^m) = S(m) = \Theta(m) = \Theta(\log u) \end{aligned}$$

5. $\text{Successor}(W, x)$

j $\leftarrow$ $\text{Successor}(\text{sub}[W][\text{high}(x)], \text{low}(x))$

if $j < \infty$ return $\text{high}(x)\sqrt{ |W| } + j$ else $i \leftarrow \text{Successor(Summary}[W], \text{high}(x))$ $j \leftarrow \text{Successor(sub}[W][i], -\infty)$

return $i \sqrt{ |W| } + j$

We make $3$ recursive calls. The running time is $\Theta((\log u)^{\log 3})$.

5. van Emde Boas Trees

1. Improvement 1: For each widget $W$, store $\min[W]$ and $\max[W]$

$\min[W] = \max[W] = -1$ if $W$ is empty 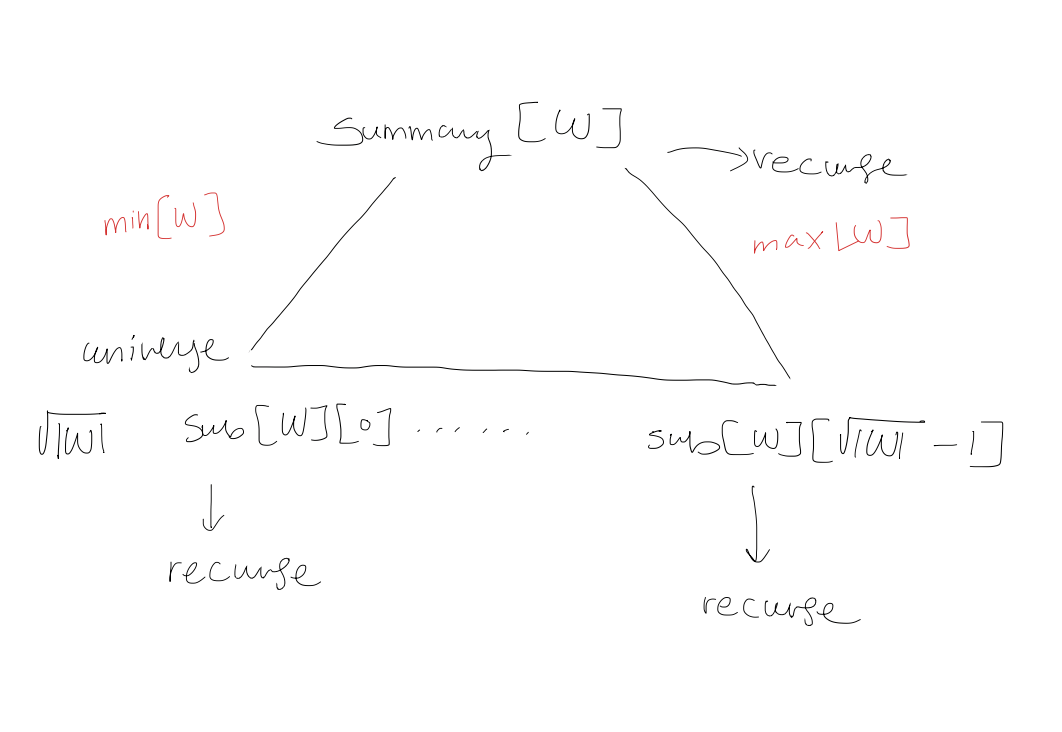$\text{Membership}: O(\log \log u)$

$\text{Successor}(W,x)$: if $x < \min[W]$ return $\min[W]$ else if $x \geq \max[W]$ return $\infty$ $W' \leftarrow \text{sub}[W][\text{high}(x)]$ if $\text{low}(x) < \max[W']$ return $\text{high}(x)\sqrt{ |W| } + \text{Successor}(W', \text{low}(x))$ else $i \leftarrow \text{Successor(Summary}[W], \text{high}(x))$ return $i \sqrt{ |W| } + \min[\text{sub}[W][i]]$

Which gives us $1$ recursive call in the worst case! $O(\log \log u)$

$\text{Insert(W, x)}$: if $\text{sub[W]}[\text{high}(x)]$ is empty $\text{Insert}(\text{Summary}[W], \text{high}(x))$ $\text{Insert(sub}[W][\text{high}(x)], \text{low}(x))$ if $x < \min[W]$ or $\min[W] = -1$: $\min[W] \leftarrow x$ if $x > \max[W]$ $\max[W] \leftarrow x$

2. Improvement: do not store $\min[W], \max[W]$ in any subwidgets of $W$

$\text{Membership}$: trivial change $\text{Successor}$: another trivial change

$\text{Insert(W,x)}$: if $\min[W] = \max[W] = -1$: $\min[W] \leftarrow \max[W] \leftarrow x$ else if $\min[W] = \max[W]$: $(\min[W], \max[W]) \leftarrow (\min(x, \min[W]), \quad \max(x, \max[W]))$ else: if $x < \min[W]$ $\text{swap}(x, \min[W])$ else if $x > \max[W]$ $\text{swap}(x, \max[W])$ $W' \leftarrow \text{sub}[W][\text{high}(x)]$ $\text{Insert}(W', \text{low}(x)) \quad (1)$ if $\max[W'] = \min[W']$: (2) $\text{Insert}(\text{summary}[W], \text{high}(x))$

Analysis If $(2)$ is true, then $(1)$ takes $O(1)$ time. $$\begin{gathered} T(u) = T(\sqrt{ u }) + O(1) \ O(\log \log u) \end{gathered}$$ $\text{Delete}(W, x)$: if $\min[W] = -1$: return if $\min[W] = \max[W]$: if $\min[W] = x$ $\min[W] \leftarrow \max[W] \leftarrow -1$ return if $\min[\text{summary}[W]] = -1$: if $\min[W] = x$: $\min[W] \leftarrow \max[W]$ else if $\max[W] = x$: $\max[W] \leftarrow \min[W]$ return if $\min[W] = x$: $j \leftarrow \min[\text{summary}[W]]$ $\min[W] \leftarrow \min[\text{sub}[W][j]] + j\sqrt{ |W| }$ $x \leftarrow \min[W]$ if $\max[W] = x$: $j \leftarrow \max[\text{summary}[W]]$ $\max[W] \leftarrow \max[\text{sub}[W][j]] + j\sqrt{ |W| }$ $x \leftarrow \max[W]$ $W' \leftarrow \text{sub}[W][\text{high}(x)]$ $\text{Delete}(W', \text{low}(x)) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad(1)$ if $\min[W'] = -1: \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (2)$ $\text{Delete}(\text{summary}[W], \text{high}(x))$

Time Analysis If $(2)$ is true, $(1)$ uses $O(1)$ time. $O(\log \log u)$.

Space Analysis $$S(u) = (\sqrt{ u } + 1)S(\sqrt{ u }) + \Theta(\sqrt{ u }) = O(u)$$ $\rightarrow\Theta(\sqrt{ u })$: pointers, min\max

What if $\sqrt{ u }$ is not an integer? $\rightarrow$ Then, each subwidget has size $\lceil \sqrt{ u} \rceil$ $$\begin{aligned} T(u) &= T(\lceil \sqrt{ u } \rceil ) + O(1) \ & \leq T(u^{2/3}) + O(1) \ &= O(\log \log u) \end{aligned}$$

6. X-fast Trie

1. Preliminary approach

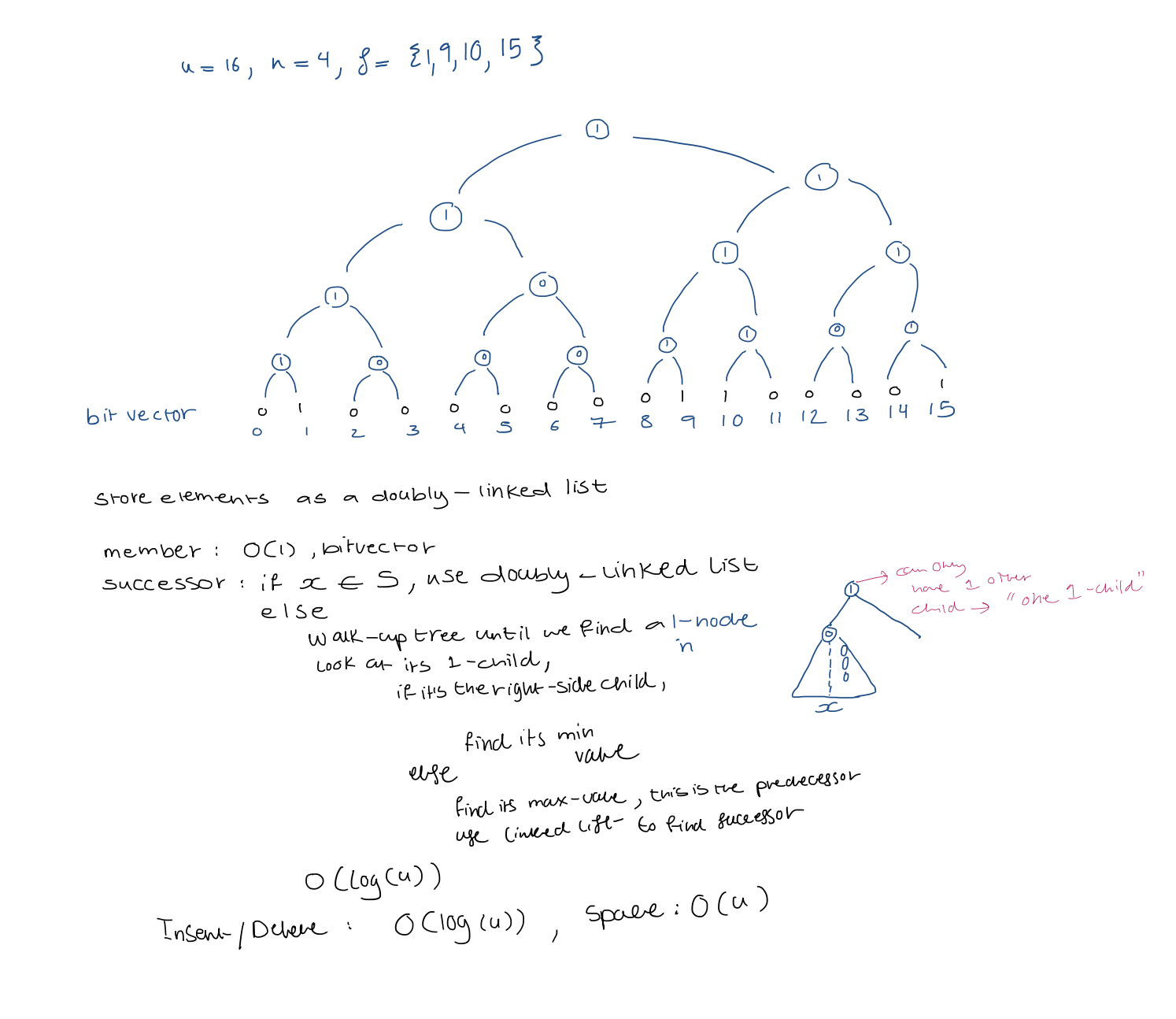
2. X-fast trie

• Do not keep the bitvector
• Keep the doubly linked list
• Keep the $1$-nodes only 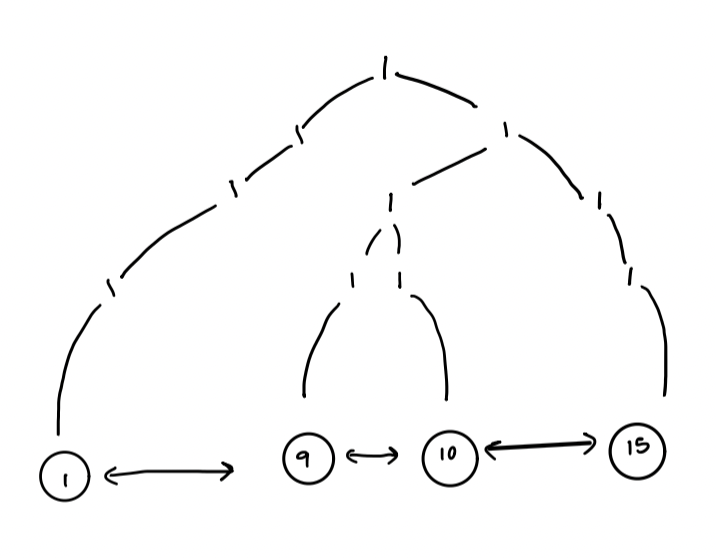Challenges:
• $\text{successor}$: How to locate the lowest 1-node on the leaf-to-node path for a 0-leaf? Solution: a) Each ancestor of leaf $x$ corresponds to a prefix of $(x)_{2}$ (the binary representation of $x$) 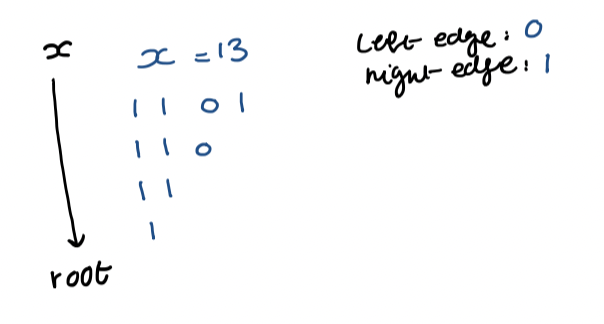b) Using such a prefix as the key for any 1-node, we store it in a dynamic perfect hash table. c) The lowest 1-node that is an ancestor of $x$ corresponds to the longest prefix of $x$ in the hash table d) Binary search in prefixes of $x$ in $O(\log \log u)$ time - If this node has a 1-child as its right child, store a descendant pointer to the smallest leaf of its right subtree ($\text{successor(x)}$) - $\text{successor(x)}$: $O(\log \log u)$ - $\text{member: } O(1)$ - $\text{insert/delete : } O(\log u)$ amortized expected time - space: list $O(n)$, hash table $O(n \log u)$, tree $O(n \log u)$

Dynamic perfect hashing on $m$ keys $O(m)$ space $O(1)$ worst-case $\text{member}$ $O(1)$ amortized expected $\text{insert/delete}$

3. Y-fast trie

• Indirection a) Cluster elements of $S$ into consecutive groups of size $\frac{1}{4} \log u \approx 2 \log u$ b) Store elements of each group in a balanced BST c) Maintain a set of representative elements, one per group, stored in the X-fast trie structur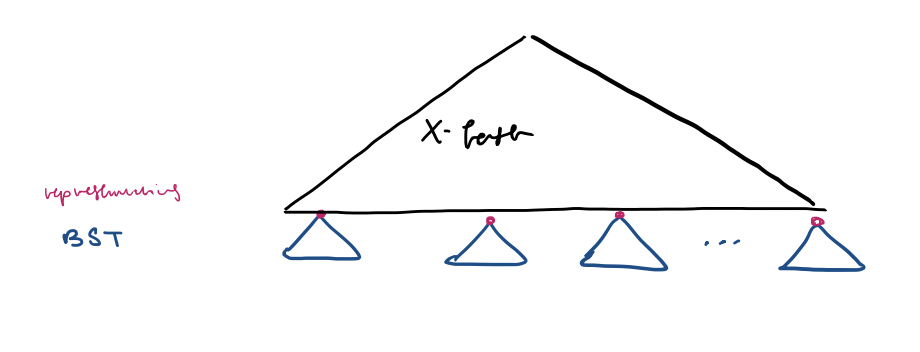e A group's representative does not have to be in $S$ but it has to be strictly between the max element in the preceding groups and the min element in succeeding groups. Space: x-fast trie: $O((\text{number of elements}) \log u) = O\left( \frac{n}{\log u} \log u \right) = O(n)$ BSTs: $O(n)$ So, overall, $O(n)$ Time: $\text{Member(x)}$ If $x$ is in the x-fast trie, it is not necessarily in $S$. Search the corresponding binary balanced search tree for $x$. If we can find it, it must be in $S$. $O(\log \log u)$. Else, Find the predecessor and successor of $x$ in the x-fast trie. $O(\log \log u)$. We check those two BSTs to look for $x$. $O(\log \log u)$. $\text{Successor(x)}$: $O(\log \log u)$ $\text{Insert/Delete(x)}$ Use the x-fast trie to locate the group that $x$ is in. Insert (or delete) $x$ into the balanced BST for that group. When a group is of size $2 \log u$, split it. If it is $< \frac{1}{4} \log u$, merge it with an adjacent group (this might cause another split). Split/merge: $O(\log u)$ amortized expected time This takes $\Omega(\log u)$ inserts/deletes Total: $O(\log \log u)$ amortized expected time