Succinct Data Structures
1. Number of trees on $n$ nodes
- Binary trees
Catalan number $$C_{n} \equiv \frac{\binom{2n}{n}}{n+1}$$ 2. Ordinal trees
Defined as $$\text{child }1, \text{ child } 2, \text{ child } 3, \ \dots$$ To count the number of ordinal trees, we construct a mapping between ordinal trees and binary trees. The left child of every node will be the first child in the ordinal tree, but the the right child corresponds to the immediately right sibling.
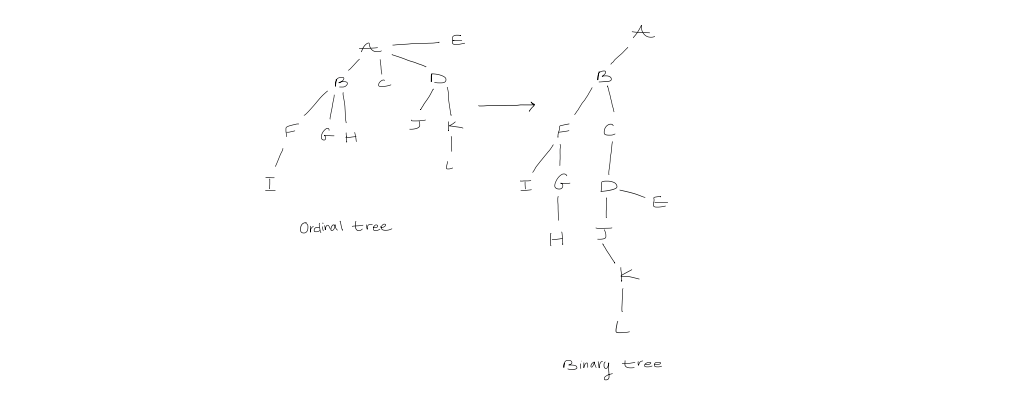
2. Information-theoretic lower bound of representing a binary tree
- Definition of information-theoretic lower bound
Given a combinatorial object of $n$ elements where $u$ is the number of different such objects of size $n$, the information theoretic lower bound on the number of bits needed to represent such an object is $\log u$ bits (because we need to be able to distinguish the $u$ different objects).
- Binary trees $$\begin{aligned} \log C_{n} &= \log\left( \frac{(2n)!}{(n!)^2} \right) - \log(n+1) \ &= \log(2n)! - 2 \log n! - \log(n+1) \ &= 2n \log(2n) - 2n \log n + o(n) & \text{(Sterling's approximation)} \ & = 2n(\log(n+1)) - 2n \log n + o(n) \ &= 2n + O(n) \end{aligned}$$ Now, recall that $$\frac{\binom{2n}{n}}{(n+1)} \approx C \cdot \frac{2^{2n}}{n^{\frac{3}{2}}}$$ This allows us to turn $2n + O(n)$ into $$2n - \frac{3}{2} \log n + O(1)$$ $\rightarrow$ Trees can be represented in $2n$ bits!
But, can we still manage to navigate them when they're represented that succinctly?
3. Level-order representation of binary trees
Append an external node for each missing child. For each node in level order, write $0$ if external, $1$ if internal
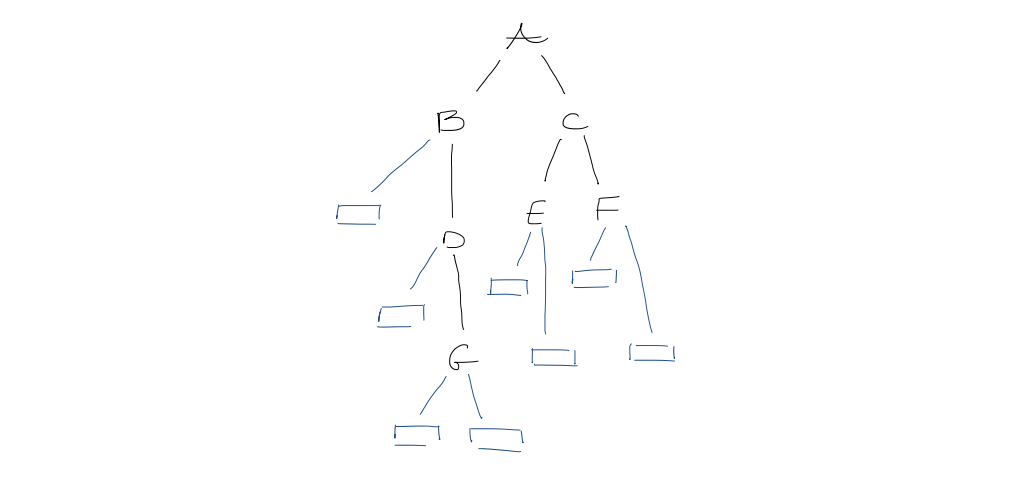
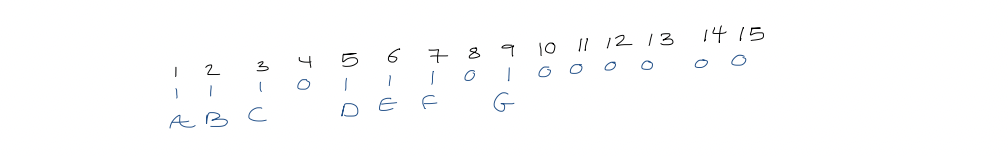
This takes $2n+1$ bits.
- Navigation
Claim: The left and right children of the $i$th internal node are at positions $2i$ and $2i+1$ in the bit vector.
Proof:
Induction on $i$.
This is clearly true for $i=1$ (root). For $i > 1$, by the induction hypothesis, the children of the $(i-1)$st internal node are at positions $2(i-1) = 2i - 2$ and $(2(i-1)) + 1 = 2i-1$.
Visually, this presents us with two cases:
- The $(i-1)$st and $i$th internal nodes are the same level
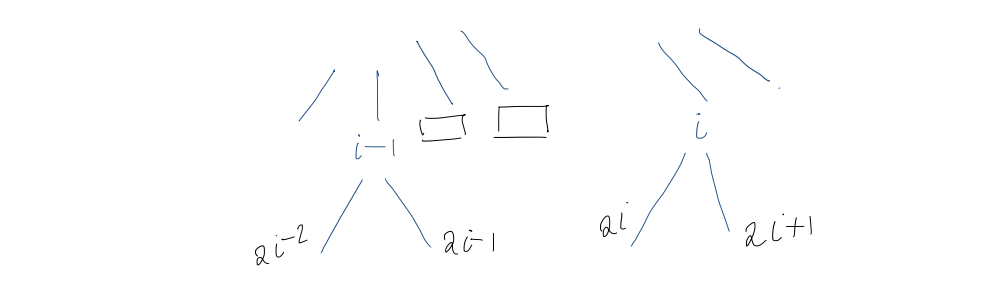
- The $(i-1)$st and $i$th internal nodes are not on the same level
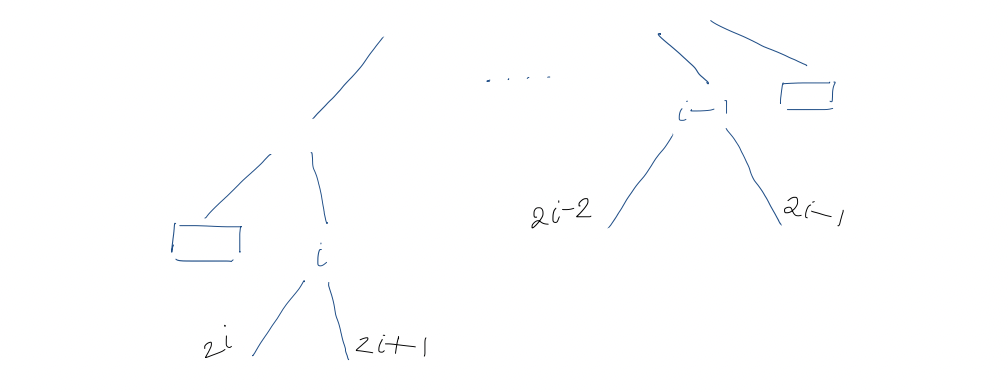
Level ordering is preserved in children, i.e. $A$'s children precede $B$'s children in level order $\iff$ $A$ precedes $B$ in level order. All nodes between the $(i-1)$st internal node and the $i$th internal node are external nodes with no children, so the children of the $i$th internal node immediately follow children of the $(i-1)$st. So, they must be at positions $2i$ and $2i+1$.
Using the following definitions of rank and select $\text{rank}{1}(i) =$ the number of $1$s up to and including position $i$ $\text{select}{1}(j) =$ the position of the $j$th $1$-bit
We can identify each node by its position in the bit vector as $\text{left-child}(i) = 2 \cdot \text{rank}{1}(i)$ $\text{right-child}(i) = 2 \cdot \text{rank}{1}(i) + 1$ $\text{parent}(i) = 2 \cdot \text{select}_{1}\left( \left\lfloor \frac{i}{2} \right\rfloor \right)$
But how do we implement $\text{rank}$?
First, split the bit vector into $(\log^2n)$-bit superblocks
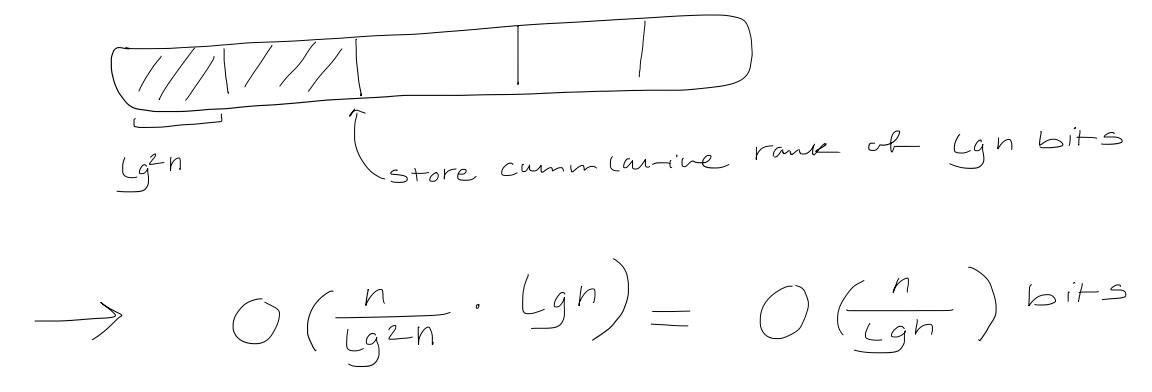 Then, split each superblock into $\frac{1}{2} \log n$-bit blocks
Then, split each superblock into $\frac{1}{2} \log n$-bit blocks
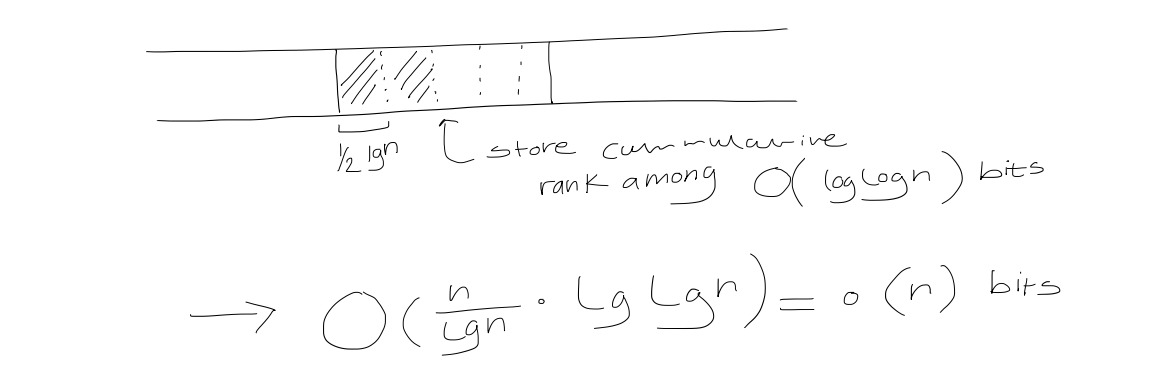 Use a lookup table for bit vectors of length $\frac{1}{2} \log n$. For any possible bit vector of length $\frac{1}{2} \log n$, and for each of its positions, store the answer.
Use a lookup table for bit vectors of length $\frac{1}{2} \log n$. For any possible bit vector of length $\frac{1}{2} \log n$, and for each of its positions, store the answer.

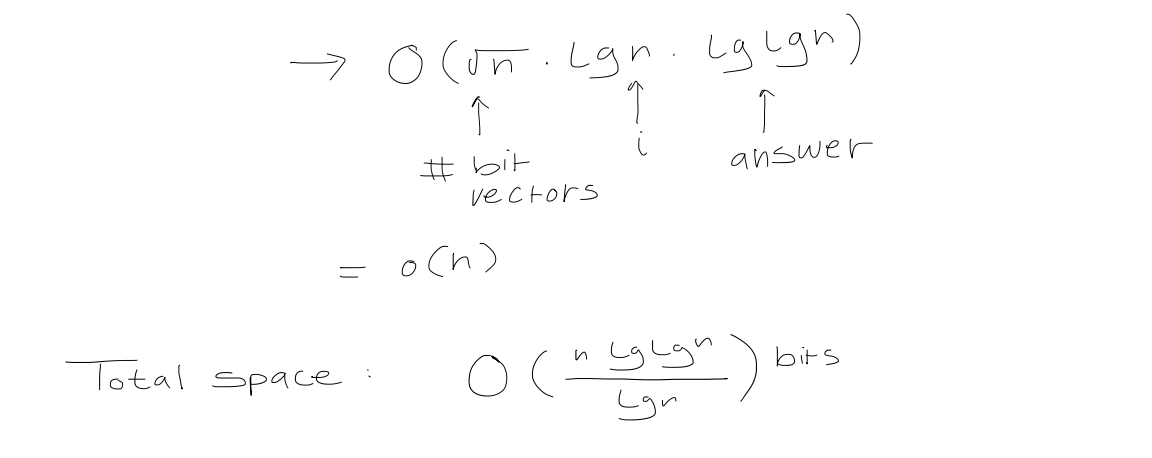 Finally, define $\text{rank}$ as $$\begin{aligned} \text{rank of superblock} \ + \quad \text{relative rank of block within superblock} \ + \quad \text{relative rank of element within block} \end{aligned}$$
Allowing us to computer it in $O(1)$ time. Note that we can follow a similar process for $\text{select}$.
Finally, define $\text{rank}$ as $$\begin{aligned} \text{rank of superblock} \ + \quad \text{relative rank of block within superblock} \ + \quad \text{relative rank of element within block} \end{aligned}$$
Allowing us to computer it in $O(1)$ time. Note that we can follow a similar process for $\text{select}$.
This allows us to conclude that we can represent a binary tree in $2n + o(n)$ bits, and access the $\text{left-child}, \ \text{right-child}, \ \text{parent}$ in $O(1)$ time.