Self-Adjusting Binary Trees

1. Problem

1. Given a sequence of access queries, what is the best way to organize the binary search tree?

2. Model

• Search must start at the root
• Cost: number of nodes inspected

3. Worst-case

$\Theta(\log n)$ upper and lower bounds

2. Static optimal BST

1. Problem

We store elements $A_{1} < A_{2} < \dots < A_{n}$. We are also given $p_{i}$, the probability of access for element $A_{i}$, and $q_{i}$, the probability of access for values between $A_{i}$ and $A_{i+1}$ (unsuccessful accesses). Also, we define $$\begin{gathered} A_{0} = -\infty, \quad A_{n+1} = \infty \ p_{0} = p_{n+1} = 0\end{gathered}$$ Let $T[i, j]$ be the root of the optimal tree on range $q_{i-1}$ to $q_{j}$. The cost of the tree rooted at $T[i,j]$ is $$\sum \text{probability of looking for one of these values (gaps) in the range} \times \text{the cost of doing this in that tree}$$

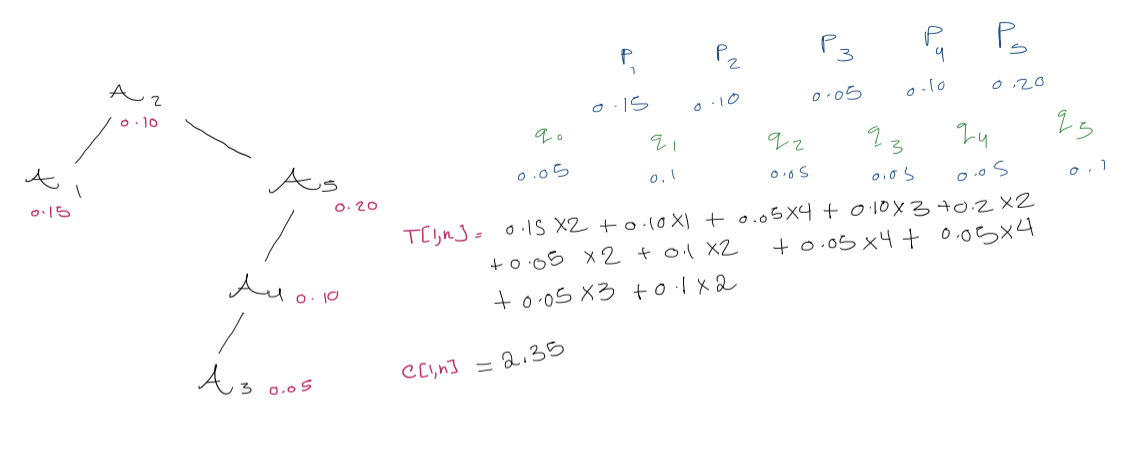
3. Dynamic programming

Observation

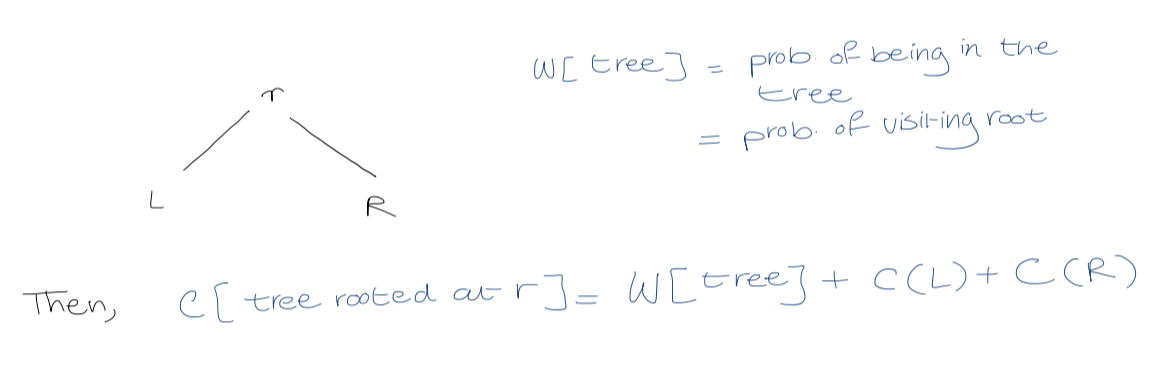
It will be handy to have $W[i,j]$, the probability of accessing any node/gap $q_{i-1}, \dots, q_{j}$ or $p_{i}, \dots, p_{j}$. $$W[i,j] = \sum_{k=i}^j p_{k} + \sum_{k= i-1}^j q_{k}$$ $$W[i, j+1] = W[i, j] + p_{j+1} + q_{j+1}$$ All the entries of $W[i,j]$ can be computed in $O(n^2)$ time. #final why are we adding the probabilities to get the cost? $$C[i,j] = \cases{0 \quad \text{if} \quad j = i-1 \ W[i, j] + \min_{r = i}^j (C[i, r-1] + C[r+1, j]) \quad \text{if} \quad i \leq j}$$ OPTIMAL-BST($p, q, n$) for $i \leftarrow 1$ to $n+1$ $C[i, i-1] \leftarrow 0$ $W[i, i-1] \leftarrow q_{i-1}$ for $l \leftarrow 1$ to $n$ for $i \leftarrow 1$ to $n - l +1$ $j \leftarrow i + l -1$ $C[i, j ] \leftarrow \infty$ $W[i,j] \leftarrow W[i, j-1] + p_{i} + q_{j}$ for $r \leftarrow i$ to $j$ $t \leftarrow C[i, r-1] + C[r+1, j] + W[i,j]$ if $t < C[i,j]$ $C[i,j] \leftarrow t$ $T[i,j] \leftarrow r$

Running time: $O(n^3)$ But $O(n^2)$ time is possible!

3. Splay trees

1. On accessing a node, we move (splay) it to the root by a sequence of local moves

2. Splaying

We let $x$ be a node being moved toward the root, $y$ be its parent, and $z$ be $y$'s parent. There are $3$ cases of splaying:

1. Zig step

If $y$ is the root, we rotate $x$ so that it becomes the root (single rotation).

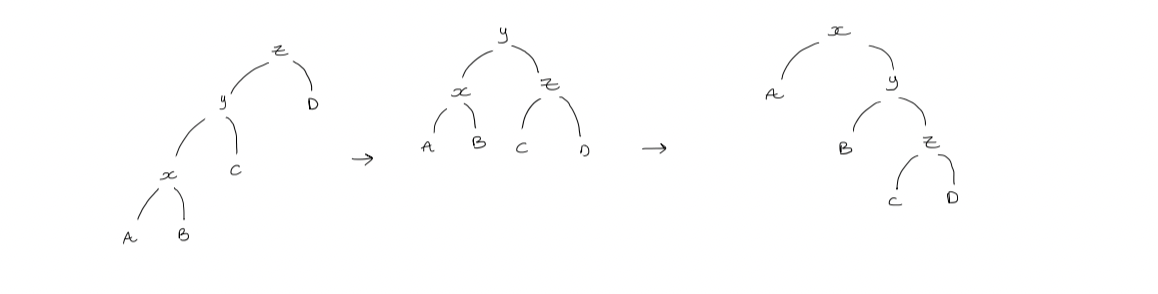
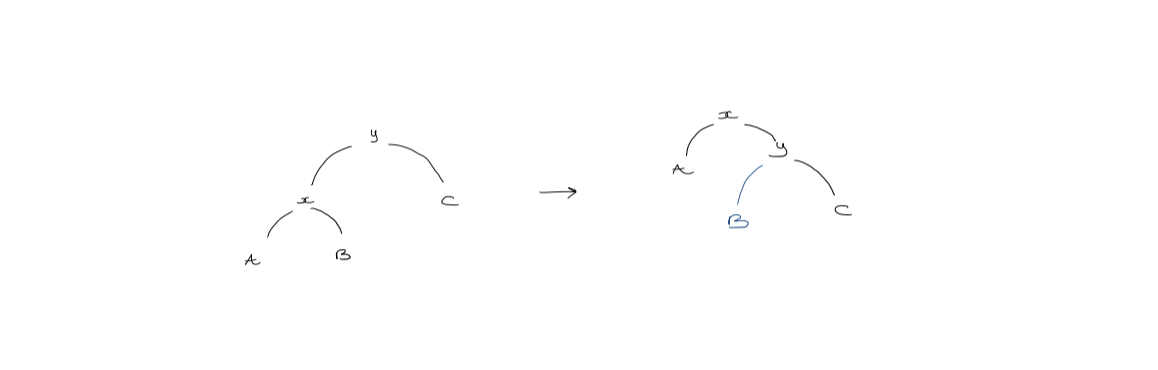2. Zig-zig step

If $y$ is not the root and $x$ and $y$ are both left or both right children, and we first rotate $y$ then rotate $x$.

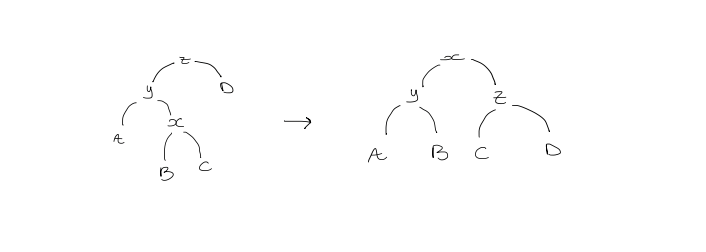
3. Zig-zag step

If $y$ is not the root, and $x$ is a left child while $y$ is a right child, or vice versa, then we double rotate $x$.

Running time analysis

• Splaying a node $x$ of depth $d$: $O(d)$

Example: single rotation of $x$ only (not splaying) 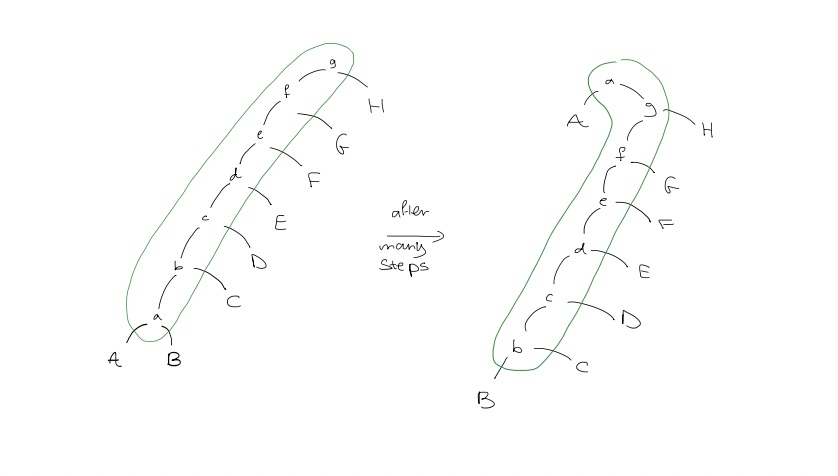Splaying 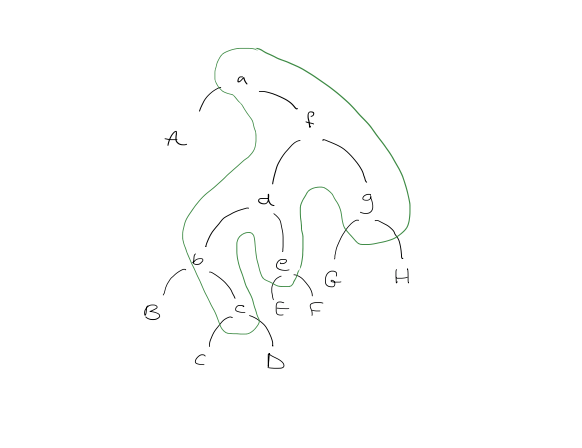Intuition: splaying roughly halves the length of the access path

Definitions:

• $w(i)$ is the weight of item $i$ (positive)
• #final are items leaves? no
• $s(x)$ is the size of a node $x$ in the tree; sum of weights of all individual items in the subtree rooted at $x$
• $r(x)$ is the rank of node $x$; defined as $\log(s(x))$
• The potential, $\phi$, of the tree is the sum of the ranks of all its nodes

Note: $\phi_{i}$ is not necessarily nonnegative $$\sum_{i=1}^nC_{i} = \sum_{i=1}^m a_{i} + \phi_{0} - \phi_{m}$$ The cost if the number of rotations.

Access lemma: the amortized time to splay a tree with root $t$ at node $x$ is at most $$3(r(t) - r(x)) + 1 = O\left( \log\left( \frac{s(t)}{s(x)} \right) \right)$$ Proof:

If there are no rotations ($x$ happens to be $t$), then the bound is immediate (cost is $0$).

So, assume that there is at least one rotation and consider the first splaying step. There are three cases for this step

1. Zig
2. Zig-zig
3. Zig-zag

Let $r_{0}(i)$, $r_{1}(i)$ and $s_{0}(i), s_{1}(i)$ represent the rank and size of node $i$ before and after the first step. Also, let $y$ be the parent $x$, $z$ be the parent of $y$.

1. Zig

$y$ is the root, so $y = t$. 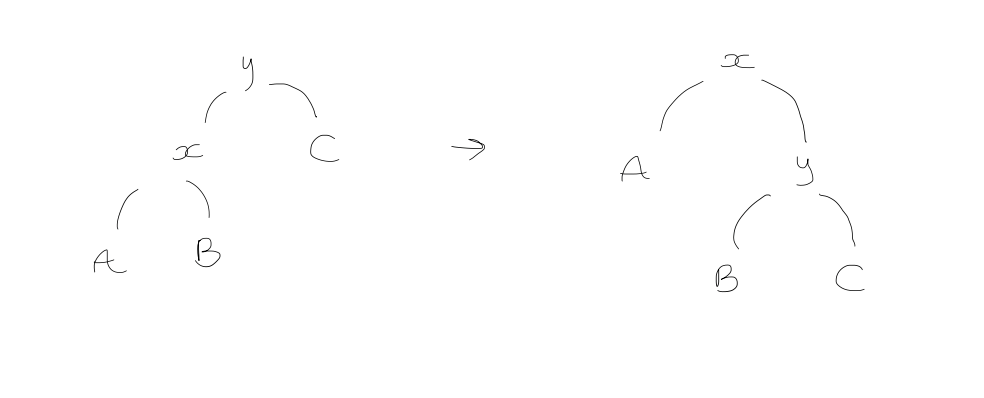The actual cost for a single rotation is just $1$. The amortized cost is

$$\begin{gathered} 1 + \phi_{1} - \phi_{0} = 1+ (r_{1}(x) + r{1}(y)) - (r_{0}(x) + r_{0}(y)) \\leq 1 + r_{1}(x) - r_{0}(x) \\leq 1 + 3(r_{1}(x) - r_{0}(x)) \end{gathered}$$

(we only include ranks of $x$ and $y$ because they're the only nodes that gain/lose descendants, the rank of $x$ increases while that of $y$ decreases)

2. Zig-zig step

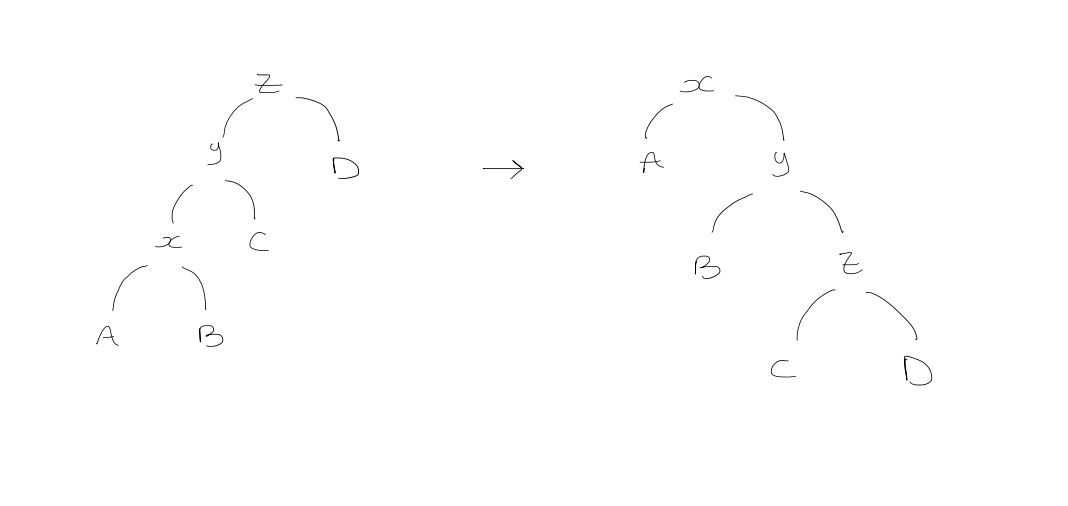Amortized cost is $$\begin{gathered} 2 + r_{1}(x) + r_{1}(y) + r_{1}(z) - r_{0}(x) - r_{0}(y) - r_{0}(z) \ = 2+ + r_{1}(y) + r_{1}(z) - r_{0}(x) - r_{0}(y) & (\text{because } r_{1}(x) = r_{0}(z)) \ \leq 2 + r_{1}(x) + r_{1}(z) - r_{0}(x) - r_{0}(x) & (\text{because } r_{1}(x) \geq r_{1}(y), \ r_{0}(x) \leq r_{0}(y)) \ \end{gathered}$$ We now show $$\begin{gathered} 2 + r_{1}(x) + r_{1}(z) - 2r_{0}(x) \leq 3(r_{1}(x) - r_{0}(x)) \iff r_{1}(z) + r_{0}(x) - 2r_{1}(x) \leq -2 \ r_{1}(z) + r_{0}(x) - 2r_{1}(x) \ = (r_{1}(z) - r_{1}(x)) + (r_{0}(x) - r_{1}(x)) \ \log\left( \frac{s_{1}(z)}{s_{1}(x)} \right) + \log\left( \frac{s_{0}(x)}{s_{1}(x)} \right) = \log\left( \frac{s_{1}(z)}{s_{1}(x)} \cdot \frac{s_{0}(x)}{s_{1}(x)}\right) \end{gathered}$$ Since $s_{1}(x) \geq s_{1}(z) + s_{0}(x)$, $$\begin{gathered} \frac{s_{1}(z)}{s_{1}(x)} + \frac{s_{0}(x)}{s_{1}(x)} \leq 1 \end{gathered}$$ Then $$\frac{s_{1}(z)}{s_{1}(x)} \cdot \frac{s_{0}(x)}{s_{1}(x)} \leq \frac{1}{4}$$ Because, apparently, $\sqrt{ ab } \leq \frac{a+b}{2}$

Therefore, $$\begin{gathered} r_{1}(z) + r_{0}(x) - 2r_{1}(x) \ \leq \log\left( \frac{1}{4} \right) \ = -2 \end{gathered}$$' Hence, the amortized cost is $\leq 3(r_{1}(x) - r_{0}(x))$

3. Zig-zag step

We double-rotate 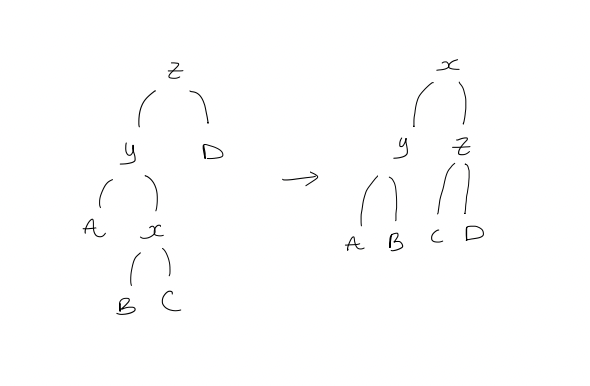Amortized cost calculation:

$$\begin{gathered} & 2 + r_{1}(x) + r_{1}(y) + r_{1}(z) - r_{0}(x) - r_{0}(y) - r_{0}(z) \ & = 2 + r_{1}(y) + r_{1}(z) - r_{0}(x) - r_{0}(y) \ \text{Since } r_{0}(x) < r_{0}(y), \ & = 2 + r_{1}(y) + r_{1}(z) - 2r_{0}(x) \ \text{We now show } 2 + r_{1}(y) + r_{1}(z) - 2r_{0}(x) \leq 3(r_{1}(x) - r_{0}(x)) \ \text{This is equivalent to }\ & r_{1}(y) + r_{1}(z) + r_{0}(x) - 3r_{1}(x) \leq -2 \ \text{Note that } \ & r_{1}(y) + r_{1}(z) + r_{0}(x) - 3r_{1}(x) = \log\left( \frac{s_{1}(y)}{s_{1}(x)} \cdot \frac{s_{1}(z)}{s_{1}(x)} \right) + r_{0}(x) - r_{1}(x)\ \text{Since } s_{1}(x) \geq s_{1}(y) + s_{1}(z), \ & \leq \log \frac{1}{4} = -2 \end{gathered}$$ Suppose a splay operation requires $k > 1$ steps, then only the $k$th (last) step can be a zig step. The amortized cost of the whole splay operation is at most $$\begin{gathered} 3r_{k}(x) - 3r_{k-1}(x) + 1 + \sum_{j=1}^{k-1}(3r_{j}(x) - 3r_{j-1}(x)) \ = 3r_{{k}}(x) - 3r_{k-1}(x) + 1 + 3r_{k-1}(x) - 3r_{0}(x) \ = 3r_{k}(x) - 3r_{0}(x) + 1 \end{gathered}$$

The Balance Theorem states that given a sequence of $m$ accesses into an $n$-node splay tree $T$, the total access time is $O((m+n) \cdot \log(n) + m)$.

Proof:

We assign a weight of $\frac{1}{n}$ to each item. Then, $$\frac{1}{n} \leq s(x) \leq 1$$

Therefore, the amortized cost of any access is at most $$\leq 3 \left( \log(1) - \log\left( \frac{1}{n} \right) \right) + 1 = 3 \log(n)+1$$ The maximum potential of $T$ is $$\begin{gathered} \sum_{i=1}^n \log(s_{i}) \leq \sum_{i=1}^n \log(1) = 0 \end{gathered}$$ The minimum potential of $T$ is $$\sum_{i=1}^n \log(s_{i}) \geq \sum_{i=1}^n \log\left( \frac{1}{n} \right) = -n \log (n)$$ Therefore, $$\phi_{0} - \phi_{m} \leq 0 - (-n \log n) = n \log n$$ And the total actual cost is $$\begin{gathered} \leq m(3 \log n + 1) + \phi_{0} - \phi_{m} \ = 3m\log(n) + m + n \log n \ = O((m+n) \log n + m) \end{gathered} $$

But what does this mean?

$\rightarrow$ If we access $m \geq n$ times, the average cost per access is $\frac{O(m \log n + m)}{m} = O(\log n)$

The Static Optimality theorem states that given a sequence of $m$ access into an $n$-node splay tree, where each item is accessed at least once, then the total access time is $O\left( m+\sum_{i=1}^n q(i) \log\left( \frac{m}{q_{i}} \right) \right)$ where $q_{i}$ is the number of times item $i$ is accessed.

Proof:

We assign a weight of $\frac{q_{i}}{m}$ to each item $i$. Then, $$\frac{q(x)}{m} \leq s(x) \leq 1$$ The amortized cost of $n$ accesses is at most $$\leq 3 \left( \log(1) - \log\left( \frac{q(x)}{m} \right) \right) + 1 = 3 \log\left( \frac{m}{q(x)} \right)+1$$ And $$\phi_{0} - \phi_{m} \leq 0 - \sum_{i=1}^n\log\left( \frac{q(i)}{m} \right) = \sum_{i=1}^n \log\left( \frac{m}{q(i)} \right)$$ And the total actual cost is $$\leq 3 \sum_{i=1}^n q(i) \log\left( \frac{m}{q(i)} \right) + m + \sum_{i-1}^n \log\left( \frac{m}{q(i)} \right) \leq O\left( m + \sum_{i=1}^n q(i) \log\left( \frac{m}{q(i)} \right)\right)$$

We define the following as the entropy of access $\times m$ $$\sum_{i=1}^nq(i) \log\left( \frac{m}{q(i)} \right)$$

3. Update

Insertion

1. Insert as a new leaf
2. Splay at the new node (the leaf that got turned into a node?)

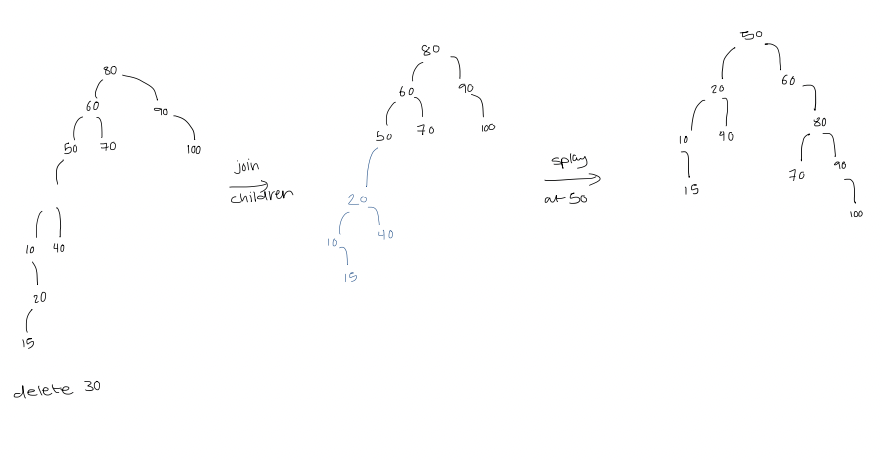
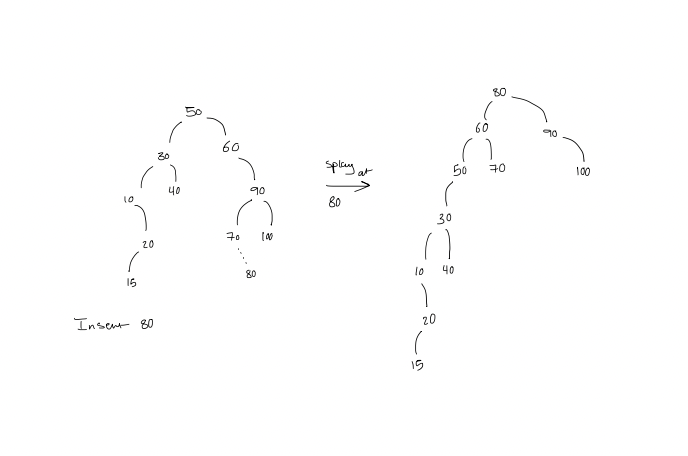Deletion

1. Delete the node (creating 3 disconnected trees)
2. Splay the largest value in its left subtree
3. The right subtree becomes a subtree of the new root of the left subtree
4. Replace the deleted node by the new root of these two subtrees connected together
5. Splay at $x$'s parent