Resizable Arrays

Definition: A resizable array $A$ represents $n$ fixed-size elements, each assigned a unique index from $0$ to $n-1$ to support $\text{Locate}(i)$: determines the location of $A[i]$ $\text{Insert}(x):$ store $x$ in $A[n]$, and increment $n$ $\text{Delete}$: discard $A[n-1]$, decrementing $n$

Vector?

1. No deletion

Strategy: upon inserting an element into a full array, allocate a new array with twice the size, and copy all the elements, including the new one, over. Define: $n$: the number of elements in $A$ $s$: the capacity of $A$ Load factor $\alpha = \frac{n}{s}$ when $A$ is nonempty, and $=1$ otherwise. $\alpha$ is always $\geq \frac{1}{2}$

Pseudocode: $\text{Insert}(x)$: If $s=0$ allocate $A$ with $1$ slot $s \leftarrow 1$ If $n=s$ allocate $A'$ with $2s$ slots copy all elements of $A$ into $A'$ deallocate $A$ $A' \leftarrow A$ $s \leftarrow 2s$ $A[n] \leftarrow x$ $n \leftarrow n+1$

Cost analysis: Insert If $A$ is not full for the $it$th insert, we simply copy one element, and the cost is $1$. Otherwise, the cost is $i$ because we copy $i$ elements.

[[Amortized Analysis]]: Let $A_{i}$ denote the array $A$ after the $i$th insert. What should we define our potential as? Idea 1: $\phi(A_{i}) = n$ Problem: $\phi(A_{i}) - \phi(A_{i-1}) = 1$ Idea 2: $\phi(A_{i}) = n-s$ Problem: $\phi(A_{i}) \leq 0$ Idea 3: $\phi(A_{i}) = 2n - s$ $\phi(A_{0}) = 0$ And $\phi(A_{i}) \geq 0$ for all $i$ ==Good!==

To analyze the amortized cost, $a_{i}$, of the $i$th insert, let $n_{i}$ denote the number of elements stored in $A_{i}$ and $S_{i}$ denote the total size of $A_{i}$.

Now, we need to consider two cases: 1. The $i$th insert does not require the array to be reallocated Then $S_{i} = S_{i-1}$ Thus, $$\begin{aligned}a_{i} &= C_{i} + \phi(A_{i}) - \phi(A_{i-1})\ &= 1 + (2n_{i} - S_{i}) - (2n_{i-1} - S_{i-1}) \ &= 1 + (2(n_{i-1} + 1) - s_{i-1}) - (2n_{i-1} - S_{i-1}) \ &= 3\end{aligned} $$ 2. The $i$th insert requires a new array to be allocated. Then $S_{i} = 2S_{i-1}$ and $S_{i-1} = n_{i-1}$ And thus $$\begin{aligned}a_{i} &= C_{i} + \phi(A_{i}) - \phi(A_{i-1}) \ &= n_{i} + (2n_{i} - s_{i}) - (2n_{i-1} - S_{i-1})\ &= n_{i-1} + 1 + (2(n_{i-1} + 1) - 2n_{i-1}) - (2n_{i-1} - n_{i-1}) \ &= 3 \end{aligned}$$

Therefore, the insert operation is $O(1)$ amortized time.

What about Delete? Idea 1: When $\alpha$ is too small, allocate a new, smaller array and copy the elements from the old array to the new array. Problem: Would not achieve $O(1)$ amortized time. Idea 2: Double the array size when inserting into a full array, halve the array size when deletion would cause the array to be less than half-full. Counterexample: For simplicity, assume $n$ is a power of $2$. The first $\frac{n}{2}$ operations are insertions, which cause $A$ to be full. The next $\frac{n}{2}$ are insert, then two deletes, then two inserts, two deletes, etc. Leading us to spend $\Theta(n)$ time every two operations, and an overall running time of $\Theta(n^2)$ Idea 3: We need to introduce more slack, what if we only half the size of the array when a deletion causes the array to be less than a quarter-full?

Analysis: Define $\alpha_{i}$ to be the load factor after the $i$th operation $$\phi(A_{i}) = \begin{cases} 2n_{i} - S_{i} \quad \text{if} \quad \alpha_{i} \geq \frac{1}{2} \ \ \frac{S_{i}}{2} - n_{i} \quad \text{if} \quad \alpha_{i} < \frac{1}{2} \ \end{cases}$$ We now consider two cases: 1. The $i$th operation is insert (exercise: what four cases did we eliminate here?) 1. $\alpha_{i-1} \geq \frac{1}{2}$ and a new array is allocated 2. $\alpha_{i-1} \geq \frac{1}{2}$ and no new array is allocated 3. $\alpha_{i-1} < \frac{1}{2}$ and $\alpha_{i} < \frac{1}{2}$ 4. $\alpha_{i-1} < \frac{1}{2}$ and $\alpha_{i} \geq \frac{1}{2}$ 2. The $i$th operation is delete 1. $\alpha_{i-1} < \frac{1}{2}$ and a new array is allocated 2. $\alpha_{i-1} < \frac{1}{2}$ and no new array is allocated 3. $\alpha_{i-1} \geq \frac{1}{2}$ and $\alpha_{i} \geq \frac{1}{2}$ 4. $\alpha_{i-1} \geq \frac{1}{2}$ and $\alpha_{i} < \frac{1}{2}$

Let's do case 2.1 $n_{i} = n_{i-1} - 1$ $S_{i-1} = 4n_{i-1}$ $S_{i} = \frac{S_{i-1}}{2} = 2n_{i-1}$ $\alpha_{i} = \frac{n_{i}}{S_{i}} = \frac{n_{i-1} - 1}{2n_{i-1}} < \frac{1}{2}$ $a_{i} = C_{i} + \phi(A_{i}) - \phi(A_{i-1})$ $= n_i + \frac{S_{i}}{2} - n_{i} - \left( \frac{S_{i-1}}{2} - n_{i-1} \right)$ $= (n_{i} -1) + n_{i-1} - (n_{i-1} -1) - 2n_{i-1} + n_{i-1}$ $= 0$

Why do we have a factor of $\frac{1}{2}$ in our piecewise definition of $\phi(A_{i})$? Try $C(S_{i} - 2n_{i})$ where $C$ is a constant and show why $\frac{1}{2}$ is the best.

Overhead: The overhead of a data structure currently storing $n$ elements is the amount of memory usage beyond the minimum required to store $n$ elements. Example: Vector

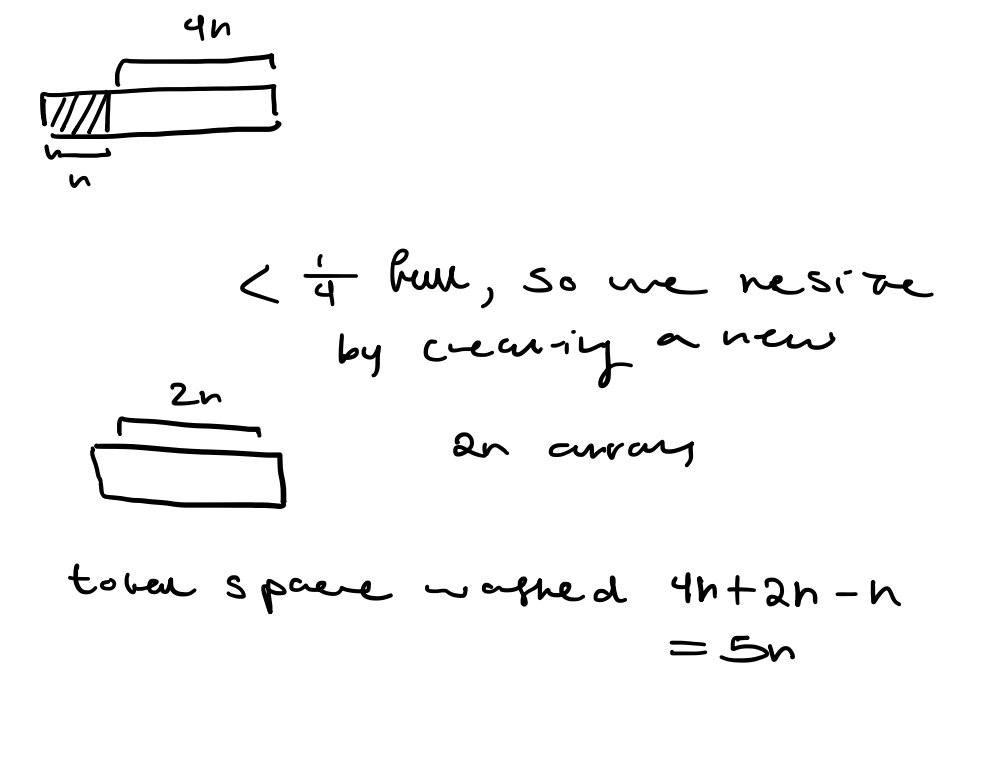
Lower bound Claim: At some point in time, $\Omega({\sqrt{ n }})$ overhead is necessary for any data structure that supports ==inserting== elements and ==locating== any of those elements in some order, where $n$ is the ==number of elements currently stored in the data structure.== Proof: Consider the following sequence of operations for any $n$: $Insert(a_{1}), Insert(a_{2}), Insert(a_{3}), \dots Insert(a_{n})$ After inserting $a_{n}$, let $k(n)$ be the number of memory blocks occupied by the data structure and $S(n)$ be the size of the largest of those blocks. Hence, $S(n)\cdot k(n) \geq n$. 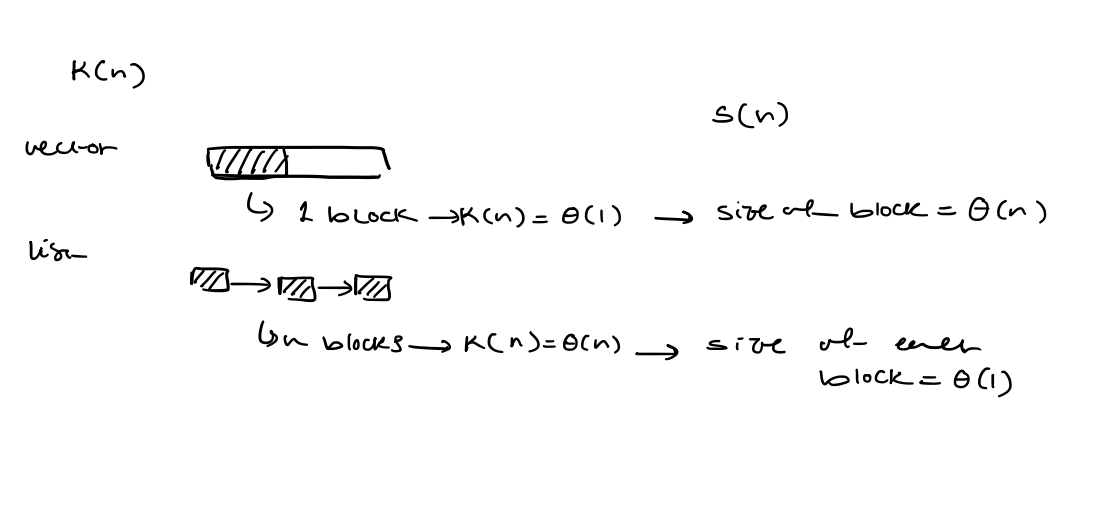At this time, the overhead is at least $k(n)$ to store bookkeeping information (e.g. address) for each block. Furthermore, after the allocation of the block of size $S(n)$, the overhead is at least $S(n)$ The worst-case overhead is at least $\max(S(n), k(n))$. Since $S(n) \cdot k(n) \geq n$, at some point, the overhead is at least $\sqrt{ n }$ (==because like we just stated, the overhead is the larger of the two and their product is larger than $n$)==.

An optimal solution Model: RAM $Allocate(S)$: Returns a new block of size $S$. $\rightarrow O(1)$ ($O(s)$ if initialization required) $Deallocate(B)$: Free the space used by the given block. $B$ $\rightarrow O(1)$ ($O(s)$ if initialization required) $Reallocate(B, S)$: If possible, resize block $B$ to size $S$. Otherwise, allocate a block of size $S$, copy the content of $B$ into a new block, and deallocate $B$. $\rightarrow O(s)$

Two approaches that do not work

1. Try to store elements in $\theta(\sqrt{ n })$ blocks, where the size of the largest block is $\theta(\sqrt{ n })$

Issues: $locate(i)$: the element is in the $\left\lceil \frac{\sqrt{ 1 + 8i } - 1}{2} \right\rceil$th block and the ==RAM model is not naturally equipped with $\sqrt{ x}$.==

$locate(i)$ Block: number of bits in ($i+1$)$_{2} - 1$ Issue: the size of the largest block is $\theta(n)$

Solution: combine two ideas Index block: Data blocks: - Index block: pointers to data blocks - Data blocks $(DB_{0}, DB_{1}, \dots, DB_{d-1})$: elements - Super blocks $(SB_{0}, SB_{1}, SB_{s-1})$ - Data blocks are grouped into super blocks - Data blocks in the same superblock are of the same size - When $SB_{k}$ is fully allocate, it consists of $2^{\lfloor k/2\rfloor}$ data blocks, each of size $2^\left\lceil \frac{k}{2} \right\rceil$ - Size of $SB_{k}$ is $2^k$ - Only $SB_{s-1}$ might not be fully allocated

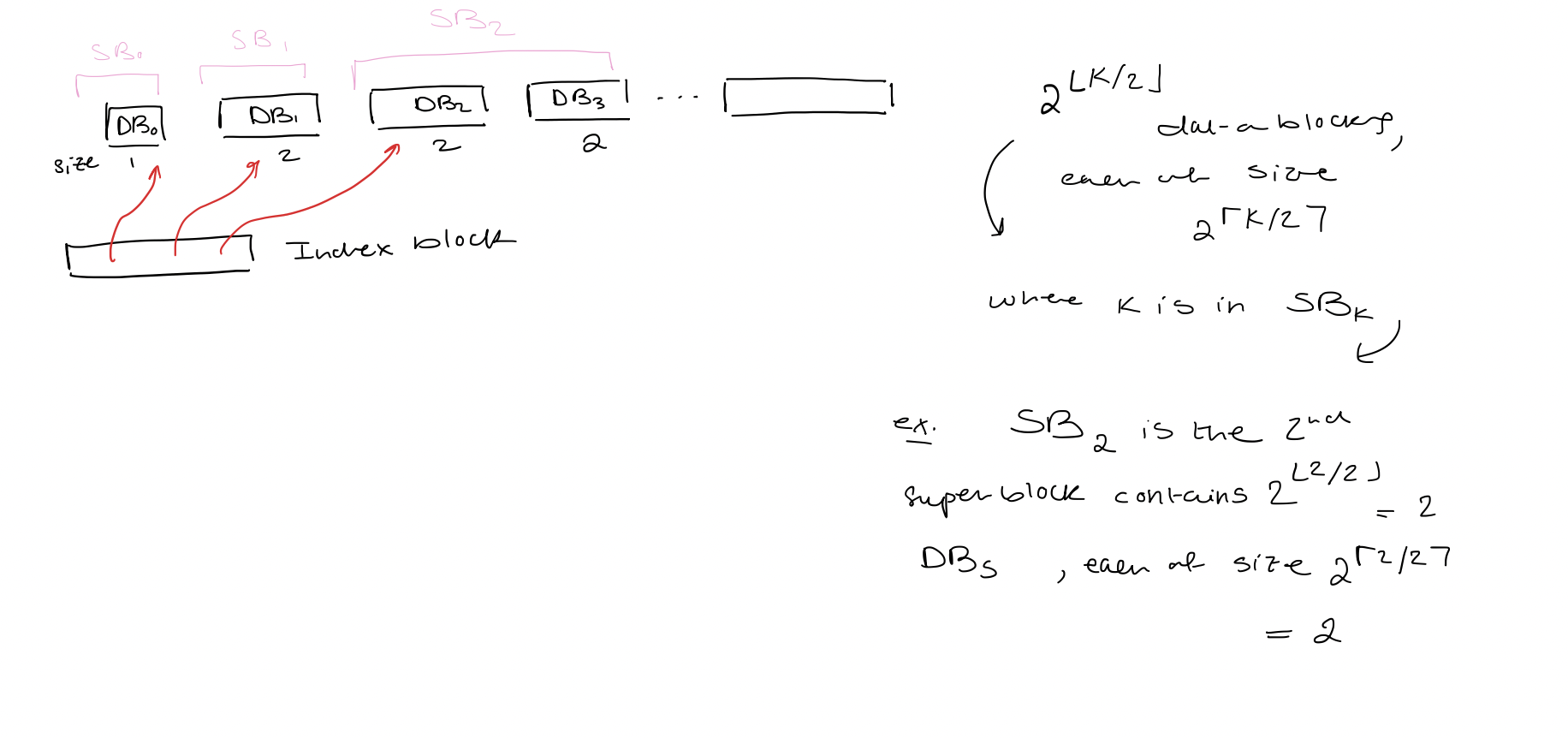Locate($i$)

$\rightarrow$ Let $r$ denote the binary expression of $i+1$ without leading $0$s. $\rightarrow$ Element $i$ is element $e$ of data block $b$ of superblock $k$. $\rightarrow$ $k = |r|-1$ $\rightarrow$ $b$ is $\left\lfloor \frac{k}{2} \right\rfloor$ bits of $r$ immediately after the leading $1$ bit $\rightarrow$ $e$ is the last $\left\lceil \frac{k}{2} \right\rceil$ bits of $r$ $\rightarrow$ The number of data blocks in superblocks before $SB_{k}$ is $$p = \sum_{j=0}^{k-1} 2^{\lfloor j/2 \rfloor}$$ depending on whether $k$ is even or odd we use different geometric series $$= \cases{2\cdot\left( \frac{2^k}{2} - 1 \right)\text{ if $k$ is even} \ 3 \cdot {2}^{(k-1)/2} - 2 \text{ otherwise}}$$ $\rightarrow$ Return the location of element $e$ in data block $DB_{p+b}$ (the $b$th data block in the super block plus the offset)

Updates

• Some easy-to-maintain bookkeeping information
  • $n, s, d$ (nonempty)
  • The number of empty data blocks $(0 \text{ or } 1)$
  • Size and occupancy of the last nonempty data block, data block, the last superblock, the index block
    • The index block is maintained as a vector
  • $Insert(x)$

a) If $SB_{s-1}$ is full, we increment $s$ by $1$ b) If $DB_{d-1}$ is full, and there is no empty data block, we increment $d$ by $1$ and allocate a new data block $DB_{d-1}$ c) If $DB_{d-1}$ is full and there is an empty data block, increment $d$ by $1$ and $DB_{d-1}$ is set to be an empty data block (?)

Store $x$ in $DB_{d-1}$

• Delete:
  • Remove the last element from $DB_{d-1}$
  • If $DB_{d-1}$ is empty
    • $d \leftarrow d-1$
    • If there is another empty data block, we deallocate it
  • If $SB_{s-1}$ is empty, we decrement $s$ by $1$.

Space Bound

• $S = \lceil \log(1 + n) \rceil$ Proof The number of elements in the first $s$ superblocks is $\sum_{i=0}^{s-1} 2^i = 2^s - 1 \text{ (geometry series)}$ If we let this equal $n$, then $s = \log(1+n)$ For slightly smaller $n$, the same number of superblocks is required. Hence, we take the ceiling.
• The number of data blocks is $O(\sqrt{ n })$
  • There is at most one empty data block, so it is sufficient to only consider the number of nonempty data blocks $d = O(\sqrt{ n })$
  • $d \leq \sum_{i=0}^{s-1}2^{\lfloor i/2\rfloor} \leq \sum_{i=0}^{s-1}2^{i/2} = \frac{2^{s/2} - 1}{\sqrt{ 2 } - 1} \text{ (geometry series) }$
  • $2^s = O(n)$ so, $2^{s/2} = O(\sqrt{ n })$
• The last (empty or nonempty) data block has size $\theta(\sqrt{ n })$ Proof The size of $DB_{d-1} = 2^{\lceil (s-1)/2 \rceil} = \theta(\sqrt{ n })$ If there is an empty data block, it either has the same size or twice the size. Total overhead: $O(\sqrt{ n })$

Update time

• If allocate or deallocate is called when $n= n_{0}$ then the next call to allocate or deallocate will occur after $\Omega(\sqrt{ n_{0} })$ operations (this guarantees $O(1)$ amortized time even if initialization is needed). Proof: Immediately after allocating or deallocating a data block, there is exactly one empty data block. We only deallocate a data block when two are empty, so we must call Delete at least as many times as the size of the largest nonempty data block $DB_{d-1}$ which is $\Omega(\sqrt{ n_{o} })$. We only allocate a data block when this data block is full, which requires $\Omega(\sqrt{ n_{o} })$ insertions.